Himmlische Koordinaten
Der Himmel ist mit Koordinatennetzen überzogen.
Am wichtisten ist das äquatoriale System. Jeder Stern besitzt darin eine sogenannte "Rektaszension" und eine "Deklination".
Das ist ein wenig so, wie sich die Lage eines Orts auf Erden mit dessen geografischer Länge und Breite beschreiben lässt. Allerdings bewegen sich Himmelsobjekte gegenüber dem Koordinatensystem und auch das Koordinatensystem selbst ist nicht fix. Es hängt nämlich am Frühlingspunkt, der langsam die Ekliptik entlang schreitet.
Will man den Ort eines Objekts an der Himmelskugel angeben, nennt man also:
- den Zeitpunkt der Messung (Tag, Uhrzeit, Zeitzone)
- die Epoche des Koordinatensystems (Jahr)
- die Koordinate Rektaszension (gemessen vom Frühlingspunkt)
- die Koordinate Deklination (gemessen vom Himmelsäquator)
Diese Koordinaten bestimmt man aus dem Himmelsfoto.
Um von einer Epoche in die andere umzurechnen, kann man Robert Martin Ayers webbasiertes Java-Tool verwenden: Astronomical Coordinate Calculator.
Umrechnung dezimal in sexagesimal
Beim PlateSolve kann man sich die Koordinaten gleich in der hexagesimalen Schreibweise anzeigen lassen - und zwar mit Stellen hinterm Komma (z.B. 16 23 12.4 +23 45 59.2). In diesem Fall brauchen Sie hier nicht weiter zu lesen.
Der All Sky Plate Solver schneidet hinter dem Komma leider sofort ab, was in Rektaszension viel zu viel Auflösung kostet.
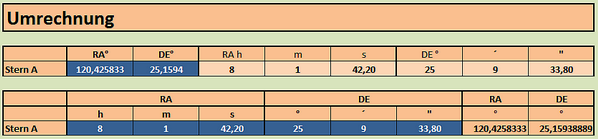
Tipp: Vereinfachen Sie die Umrechnerei mit Ihrer Tabellenkalkulation
Der All Sky Plate Solver liefert seine Koordinaten aber auf Wunsch in der Dezimalschreibweise ("copy coord as decimals"). Die Rektaszension wird dann allerdings in Dezimalgrad genannt. Um daraus die üblichen Stundenschreibweise zu erhalten, muss die Zahl durch 15 dividiert werden. Bei der Deklination entfällt diese Division.
Beispiel: 305,8778780° durch 15 = 20,391858 h
Um weiter ins vertrautere hexagesimale System umzurechnen, darf man einen wissenschaftlichen Taschenrechner zur Hand nehmen. Die einschlägige Funktion mag auf dessen Tastatur z.B. mit "DD>DMS" gekennzeichnet sein.
Ansonsten geht man so vor:
Die Ziffern vor dem Komma geben die RA-Stunden an. Die Ziffern nach dem Komma werden mit 60 multipliziert. Die Ziffern vor dem Komma der neuen Zahl geben nun die RA-Minuten an. Die Ziffern hinterm Komma werden abermals mit 60 multipliziert: So erhält man die RA-Sekunden.
Beispiel: 20,391858 h (RA-Stunden also 20). 0,390858 x 60 = 23,511512 (RA-Minuten also 23). 0,511512 x 60 = 30,69 (das sind die RA-Sekunden). Wir erhalten also 20 h 23' 30,7"
Genauso machen wir es mit der Deklination, nur dass die anfängliche Division durch 15 hier nicht vorgenommen werden darf.
Beispiel: 34,45467 ° (DE-Grad also 34). 0,45467 x 60 = 27,2802 (DE-Minuten also 27). 0,2802 x 60 = 16,8 (da sind die DE-Sekunden). Wir erhalten somit 34°27'16,8".
Beispiel: -34,45467 ° (DE-Grad also -34). 0,45467 x 60 = 27,2802 (DE-Minuten also 27). 0,2802 x 60 = 16,8 (da sind die DE-Sekunden). Wir erhalten somit -34°27'16,8".
Am besten, man bastelt sich ein einschlägiges Excel-Sheet für die ganze Umrechnung.
Aufpassen muss man da aber bei der Funktion GANZZAHL (), die bei negativen Werten ein für uns falsches Ergebnis liefert. Deshalb wandelt man die negative Deklination vorher mit ABS () in eine positive um und setzt das Minuszeichen erst ganz am Schluss wieder vor die Gradzahl. Ich löse das mit der WENN-Funktion.
Weiter zu: Genauigkeit steigern
